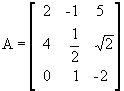Dica do dia

Rafael Andrade

Hoho #tangente

Rafael Andrade

Esta conta está correta!

Rafael Andrade

#determinantes #matrizes #Excel

Calculando #determinantes de #matrizes usando o #Excel. Um recurso tecnológico que pode ser aplicados nas aulas de matemática e que beneficiarão os alunos. As planilhas do #Excel estão disponíveis para fazer download gratuitamente.

Leia mais: http://bit.ly/183JXHS 

 

Rafael Andrade

 

Ai eu dou valor.

Rafael Andrade

Bincadeirinha *Hehe

Rafael Andrade

É melhor andar ou correr na chuva?

 Vídeo muito interessante..


Rafael Andrade

TELECURSO

O que é?

O Telecurso é uma tecnologia educacional, reconhecida pelo MEC, que oferece escolaridade básica de qualidade a quem precisa. No Brasil, ele é utilizado para a diminuição da defasagem idade-ano, Educação de Jovens e Adultos (EJA) e como alternativa ao ensino regular em municípios e comunidades distantes.
Desde 1995, a Fundação Roberto Marinho, por meio de parcerias com prefeituras, governos e instituições públicas e particulares, já implementou, em todo Brasil, 32 mil salas de aula com a Metodologia Telessala. Com essa metodologia, o professor atua como mediador de aprendizagem, utilizando, em suas aulas, os livros do Telecurso, as teleaulas e material didático complementar – cadernos de cultura, livros de literatura, dicionários, mapas. A metodologia prevê o ensino das disciplinas por módulos, e não séries, como o ensino regular no país.
Cerca de 40 mil professores já foram formados na Metodologia Telessala. Isso significa que 6 milhões de estudantes – cuja faixa etária era inadequada para a série que cursavam; ou que resolveram voltar à escola em idade adulta; ou que moravam em municípios/comunidades distantes e sem infraestrutura – concluíram o Ensino Básico.

Fonte:http://www.telecurso.org.br/o-que-e/#

Vídeos de tele-aulas do telecurso podem ser encontrados com grande  facilidade , estes servem com apoio para professores e complemento didático para alunos. Segue- se exemplos de alguns vídeos.

 Matrizes

Operações Matemáticas

Weine Roberth

Você conhece Laplace?

O famoso matemático francês Jean d'Alembert não deu a menor importância ao jovem de dezoito anos que o procurava. O rapaz enviara várias cartas de recomendação de cientistas e de políticos, e isso já bastava para deixar d'Alembert irritado. Mas ele não contava com a teimosia de Pierre Simon Laplace que, em pouco tempo, escreveu um pequeno tratado sobre os princípios gerais da Matemática e enviou-o ao professor.
Agora d'Alembert teria de mudar de opinião. Leu o trabalho do jovem Laplace e dois dias mais tarde mandou chamá-lo, dizendo-lhe: "Não costumo dar crédito a recomendações, e você não precisa delas. Você demonstrou que é digno de ser conhecido e eu lhe darei o meu apoio". Laplace conseguira a oportunidade que queria; daí em diante ele mostraria ao mundo científico que era, realmente, "digno de ser conhecido".

O menino Pierre Simon Laplace revelou logo em Beaumont-en-Auge, cidadezinha da Normandia onde nascera em Março de 1749, extraordinária inteligência. Por isso um tio seu, padre, levou-o para completar os estudos numa abadia beneditina. Daí Pierre seguiu para um colégio de Caen, onde se acentuou seu interesse pela Matemática. Aos dezoito anos, vai para Paris e, com a ajuda de d'Alembert, em pouco tempo, consegue o cargo de professor de Matemática na Escola Militar. Começa a realizar pesquisas, sobretudo em Astronomia, que impressionam a Academia de Ciências.

Estudou a fundo um dos problemas então mais atuais: a perturbação dos movimentos planetários. Temia-se, na época, que um planeta pudesse aproximar-se demais de outro, provocando uma catástrofe. Mas, com base em cálculos, Laplace demonstrou em uma série de trabalhos apresentados à Academia de Ciências que não havia motivo para tais temores, pois as irregularidades do sistema solar se corrigiram por si, durante tempos infinitamente longos.

Esses trabalhos, além de outros sobre assuntos similares, tornaram respeitado o nome de Laplace. Convidado a participar de várias academias e a lecionar nas melhores escolas, aceitava. Mas continuava estudando: dedicou-se à Química, à Física e até à Medicina, sem abandonar a Matemática e a Astronomia.

Muitas de suas teorias até hoje são válidas. Contudo, frequentes descobertas que anunciou eram baseadas em trabalhos de outros cientistas, e Laplace escondia esse fato. Isso não desmente em nada o seu gênio, confirmado por descobertas autênticas e bastante importantes; mas revela o caráter ambicioso desse homem, que usava de todos os meios para obter fama e, com ela, honras e posição social. Laplace servia-se dos grandes e os adulava. Assim, conseguiu atravessar, coberto de glórias, um tumultuado período da História francesa. O prefácio das sucessivas edições de suas obras mostra que ele fazia qualquer coisa para conseguir o beneplácito de quem estava no poder. Num prefácio de 1796, dedica seus trabalhos ao Conselho dos Quinhentos; em 1802, cobre de louvores a figura de Napoleão - que havia suprimido o Conselho - e por isso é distinguido com vários cargos políticos, entre os quais o de ministro do Interior. Mas Napoleão cai em 1814, e agora Laplace dirige suas reverências aos Bourbons, que ocupam o trono, e isso lhe vale o título de marquês, conferido por Luís XVIII. Mas era capaz também de gestos de bondade, tanto assim que ajudou vários pesquisadores pobres.

Ao morrer, a 5 de março de 1827, Laplace tinha conseguido seu objetivo: era famoso e deixara uma obra importante.

No "Tratado de Mecânica Celeste", Laplace reuniu tudo o que havia de esparso em trabalhos de vários cientistas, sobre as consequências da gravitação universal. Em outros livros, estudou os movimentos da Lua, de Júpiter e de Saturno. É famosa a sua hipótese sobre a origem dos mundos (a "Teoria de Laplace"). Explicou a formação do Universo a partir de uma nebulosa inicial, girando sobre seu próprio eixo, da qual se desprenderam, arremessados, os planetas do sistema solar. Embora hoje em dia esta seja considerada uma colocação ingênua do problema, na época serviu para despertar interesse e levantar debates.

Na Matemática, fez estudos profundos sobre a teoria das probabilidades - na obra "Teoria Analítica das Probabilidades" - e foi quem primeiro demonstrou integralmente o teorema de d'Alembert sobre as raízes das equações algébricas. Como físico, deixou estudos sobre refração, pêndulos, efeitos capilares, medidas barométricas, velocidade do som e dilatação dos corpos sólidos. E, com seu colega Lavoisier, construiu um calorímetro (instrumento para medir o calor específico dos corpos).

Fonte: Dicionário Enciclopédico Conhecer - Abril Cultural

Weine Roberth

Pérolas da matemática

Um pouco de bom humor não faz mal a ninguém!

Divirtam-se com as Perolas da matemática que estão espalhadas pela internet..

Thaís Barbosa

Revolução matemática - Cálculo Diferencial e Integral

O cálculo diferencial e integral, que Newton desenvolve ao mesmo tempo que o alemão Wilheim Leibniz (1646-1716), revoluciona a matemática.

Para se saber a área de um círculo, utilizando a nova ferramenta, basta dividir esse círculo em quadrados iguais, bem pequenos. Em seguida, calcula-se a área de um quadrado e multiplica-se pelo número total de quadrados. Com isso, acha-se a área (ou o volume, se for o caso) de qualquer figura.

Os quadrados têm de ser infinitamente pequenos para encher toda a borda do círculo, e o número de quadrados precisa ser infinito. Portanto, a área total será uma soma de infinitos termos, tipo de soma que os gregos já sabiam fazer há mais de 2 mil anos.

Thaís Barbosa

O Quociente e a Incógnita

"Às folhas tantas do livro de matemática,
um quociente apaixonou-se um dia doidamente por uma incógnita.
Olhou-a com seu olhar inumerável e viu-a, do ápice à base.
Uma figura ímpar olhos rombóides, boca trapezóide,
corpo ortogonal, seios esferóides. Fez da sua uma vida paralela a dela até que se encontraram no infinito.
"Quem és tu?" - indagou ele com ânsia radical.
"Eu sou a soma dos quadrados dos catetos,
mas pode me chamar de hipotenusa".
E de falarem descobriram que eram o que, em aritmética,
corresponde a almas irmãs, primos entre-si.
E assim se amaram ao quadrado da velocidade da luz
numa sexta potenciação traçando ao sabor do momento e da paixão retas,
curvas, círculos e linhas senoidais.
Nos jardins da quarta dimensão,
escandalizaram os ortodoxos das fórmulas euclidianas
e os exegetas do universo finito.
Romperam convenções Newtonianas e Pitagóricas e, enfim,
resolveram se casar, constituir um lar mais que um lar,
uma perpendicular.
Convidaram os padrinhos:
o poliedro e a bissetriz, e fizeram os planos, equações e diagramas para o futuro,
sonhando com uma felicicdade integral e diferencial.
E se casaram e tiveram uma secante e três cones muito engraçadinhos
e foram felizes até aquele dia em que tudo, afinal, vira monotonia.
Foi então que surgiu o máximo divisor comum,
frequentador de círculos concêntricos viciosos,
ofereceu-lhe,
a ela, uma grandeza absoluta e reduziu-a a um denominador comum.
Ele, quociente percebeu que com ela não formava mais um todo, uma unidade.
Era o triângulo tanto chamado amoroso desse problema,
ele era a fração mais ordinária.
Mas foi então que Einstein descobriu a relatividade
e tudo que era espúrio passou a ser moralidade,
como, aliás, em qualquer Sociedade ..."

Poema de Millôr Fernandes 

Thaís Barbosa

APLICAÇÕES DOS CONTEÚDOS MATEMÁTICOS

Confira na tabela as aplicações de alguns conteúdos da Matemática no nosso dia-a-dia. Conteúdo Aplicações NÚMEROS POSITIVOS E NEGATIVOS +2   -3 Temperatura: Usamos números positivos e negativos para marcar a temperatura. Se a temperatura estiver em 20 graus acima de zero, podemos representá-la por +20 (vinte positivo) . Se marcar 10 graus abaixo de zero, essa temperatura é representada por -10 (dez negativo). Conta bancária: é comum a expressão saldo negativo. Quando retiramos (débito) um valor superior ao nosso crédito em uma conta bancária, passamos a ter saldo negativo. Nível de altitude: quando estamos acima do nível do mar, estamos em uma elevação (altitude positiva). Quando estamos abaixo do nível do mar, estamos numa depressão (altidude negativa). Fuso horário: Se a abertura de uma Copa do Mundo estiver ocorrendo às 12 horas em Londres, voce estará assistindo a essa cerimônia transmitida ao vivo, pela televisão, em horário diferente. Se você estiver em São Paulo, será às 9 horas. Em Tóquio, será às 21 horas do mesmo dia. Isso ocorre de acordo com a localização de cada cidade em relação a uma referência (nesse caso, Londres), considerada o ponto zero. RAZÕES E PROPORÇÕES Razões e proporções são utilizadas em análise de dados, pesquisas, projeções e estimativas das mudanças e transformações que poderão ocorrer no Universo. TRIGONOMETRIA A trigonometria possui diversas aplicações práticas. Encontramos aplicações da Trigonometria na Engenharia, na Mecânica, na Eletricidade, na Acústica, na Medicina, na Astronomia e até na Música. Por exemplo, a trigonometria do triângulo retângulo nos permite realizar facilmente cálculos como: altura de um prédio através de sua sombra. distância a ser percorrida em uma pista circular de atletismo. largura de rios, montanhas etc. medida do raio da Terra, distância entre a Terra e a Lua. MATRIZES Muitas animações que vemos no cinema utilizam matrizes. Desde o movimento dos personagens até o quadro de fundo podem ser criados por softwares que combinam pixels em formas geométricas, que são armazenadas e manipuladas. Os softwares codificam informações como posição, movimento, cor e textura de cada pixel. Para isso, utilizam vetores, matrizes e aproximações poligonais de superfícies para determinar a característica de cada pixel. Um simples quadro de um filme criado no computador tem mais de dois milhões de pixels, o que torna indispensável o uso de computadores para realizar todos os cálculos necessários. EQUAÇÕES Quando duas linhas de um mesmo plano se cruzam, obtém-se um ponto. É comum usarmos equações para indicar a localização de pessoas, barcos, aviões, cidades. INEQUAÇÕES As inequações são usadas em experiências, estatísticas, análise de dados e comparações. EQUAÇÕES DIFERENCIAIS As equações diferenciais têm ampla aplicação na resolução de problemas complexos sobre movimento, crescimento, vibrações, eletricidade e magnetismo, aerodinâmica, termodinâmica, hidrodinâmica, energia nuclear e todo tipo de fenômeno físico que envolva as taxas de variação de quantidades variáveis.

Fonte: Só Matemática

Thaís Barbosa

Rafael Andrade

Dicas de cálculo: Como Dividir ou Multiplicar um número por 10^n

Em muitos problemas de física, ou até mesmo na matemática, encontramos valores que utilizam as potências de base 10 para simplificar a notação. Mas como trabalhar com elas?

Fique calmo, não é nenhum bicho de sete cabeças...

É mais simples do que pensamos, veja:

• Multiplicar um número por 10ⁿ:

  

Basta deslocar a vírgula n casas decimais para a direita.
Exemplo 1:  16 x 10³ = 16000
Exemplo 2:  15,567 x 10⁴ = 155670

Então, se quisermos efetuar a seguinte multiplicação: 12 x 100. Sabemos que 100=10², então:
12 x 100 = 12 x 10² = 1200.

• Dividir um número por 10ⁿ:

  

Basta deslocar a vírgula n casas decimais para a esquerda.
Exemplo 1:  16 / 10³ = 0,016
Exemplo 2:  15,567 / 10² = 0,15567

Então, se quisermos efetuar a seguinte divisão: 12 / 1000. Sabemos que 1000=10³, então:
12 / 1000 = 12 / 10³ = 0,012.

Viu só?

Com essas dicas suas multiplicações ficarão ainda mais fáceis.

Agora é só praticar.

Divirta-se!!

Thaís Barbosa

MATEMÁTICA E AS PROFISSÕES

A Matemática faz parte de quase todas as profissões. Confira na tabela abaixo as aplicações da Matemática em algumas das profissões mais tradicionais. Profissão Aplicações Administração A administração requer muito planejamento, organização e controle. Portanto, é indispensável que o administador tenha habilidade em lidar com números. Muitas vezes ele deverá preparar orçamentos para projetos, planejar e controlar pesquisas, além de resolver situações que envolvam cálculos estatísticos. O trabalho do administrador está diretamente ligado com a exatidão dos números, e por isso ele precisa ter domínio da matemática para ser bem sucedido. Agronomia Cálculo dos componentes químicos destinados à fertilização e dimensionamento das áreas a serem cultivadas. Arquitetura A matemática é fundamental para que o arquiteto possa desenvolver o seu trabalho. O arquiteto trabalha na construção de casas, edifícios, reformas, restaurações e no planejamento de bairros e cidades. A arquitetura é uma união das áreas de exatas, humanas e arte, pois exige aptidões múltiplas, como o domínio de cálculos, desenhos intuitivos e história. Cinema Muitas animações que vemos no cinema utilizam a Matemática, através da computação gráfica. Desde o movimento dos personagens até o quadro de fundo podem ser criados por softwares que combinam pixels em formas geométricas, que são armazenadas e manipuladas. Os softwares codificam informações como posição, movimento, cor e textura de cada pixel. Para isso, utilizam vetores, matrizes e aproximações poligonais de superfícies para determinar a característica de cada pixel. Um simples quadro de um filme criado no computador tem mais de dois milhões de pixels, o que torna indispensável o uso de computadores para realizar todos os cálculos necessários. Contabilidade O profissional que trabalha com contabilidade realiza muitos cálculos matemáticos, em operações envolvendo folhas de pagamento, cálculos trabalhistas e determinação de valores de impostos, assim como para elaborar o balanço comercial das empresas. Direito O profissional do Direito utiliza a Matemática quando trabalha com causas que envolvam a realização de cálculos, como por exemplo bens, valores, partilhas e heranças. Engenharia A matemática é imprescindível à formação dos engenheiros, seja qual for o seu ramo (engenharia civil, engenharia elétrica etc). É usada na construção de edifícios, estradas, túneis, metrôs, ferrovias, barragens, portos, aeroportos, usinas, sistemas de telecomunicações, criação de dispositivos mecânicos, desenvolvimento de máquinas, entre outros. Geografia Os geógrafos utilizam a Matemática em diversas situações. Existe inclusive um ramo chamado Geografia Matemática, que estuda e analisa a forma, os movimentos e as dimensões da Terra. A Matemática também é usada na topografia para medição de distâncias e ângulos, e na cartografia (estudo dos mapas) para realizar projeções cartográficas. Geologia O geólogo utiliza diversos princípios da Matemática para escavar, conhecer e avaliar os segredos do solo e das pedras. Jornalismo A Matemática é útil aos jornalistas de economia e política, além daqueles que utilizam dados estatísticos em seus trabalhos. Medicina Veterinária A modelagem matemática contribui no planejamento terapêutico e cirúrgico de diversas doenças, além de ajudar no desenvolvimento de modelos para a dinâmica do sistema cardiovascular e do sistema respiratório. A matemática auxilia ainda em pesquisas genéticas, como por exemplo pela teoria da probabilidade, que permite descobrir as chances de se obter determinado resultado proveniente de um cruzamento. É bastante útil também na análise do crescimento de populações de vírus e bactérias, através de curvas exponenciais ou logísticas, determinando o impacto de epidemias, ou ainda o crescimento de "culturas" de bactérias. Música Os teóricos da música com frequência usam a matemática para entender a estrutura musical e comunicar novas maneiras de ouvir música. Usam a Matemática também para entender as escalas musicais, sendo que alguns compositores incorporaram a proporção áurea e o número de Fibonacci em seu trabalho.  Odontologia O dentista utiliza a Matemática para calcular composições de amálgamas, posologias, doses de anestésicos e também para dimensionar próteses e aparelhos corretivos. Psicologia O psicólogo utiliza a Matemática para a análise de dados estatísticos e avaliação de testes.

Thaís Barbosa

Como é calculado o dígito verificador do CPF?

       O CPF (Cadastro de Pessoas Físicas), emitido pela Receita Federal, é caracterizado por uma função entre o conjunto das pessoas físicas cadastradas e o conjunto dos documentos emitidos.

Ou seja, o fato de um número de CPF ser autenticado pelos seus dígitos verificadores, não o torna um CPF válido, pois é necessário que ele esteja cadastrado no banco de dados da Receita Federal. Assim, um número válido de CPF nem sempre será um documento já emitido. Porém, os dígitos verificadores servem para alertar que o número foi escrito de forma inadequada, sem precisar acessar o banco de dados da Receita Federal.

Regra Prática

   

    O número de um CPF tem 9 algarismos e mais dois dígitos verificadores, que são indicados após uma barra. Logo, um CPF tem 11 algarismos. O número do CPF é escrito na forma ABCDEFGHI / JK ou diretamente como ABCDEFGHIJK, onde os algarismos não podem ser todos iguais entre si.

O J é chamado 1° dígito verificador do número do CPF.

O K é chamado 2° dígito verificador do número do CPF.

Primeiro Dígito

  Para obter J multiplicamos A, B, C, D, E, F, G, H e I pelas constantes correspondentes:

A	B	C	D	E	F	G	H	I
x10	x9	x8	x7	x6	x5	x4	x3	x2

 O resultado da soma, 10A + 9B + 8C + 7D + 6E + 5F + 4G + 3H + 2I, é dividido por 11.

 Analisamos então o RESTO dessa divisão:

 Se for 0 ou 1, o dígito J é [0] (zero). Se for 2, 3, 4, 5, 6, 7, 8, 9 ou 10, o dígito J é [11 - RESTO]

Segundo Dígito

    Já temos J. Para obter K multiplicamos A, B, C, D, E, F, G, H, I e J pelas constantes correspondentes:

A	B	C	D	E	F	G	H	I	J
x11	x10	x9	x8	x7	x6	x5	x4	x3	x2

 O resultado da soma, 11A + 10B + 9C + 8D + 7E + 6F + 5G + 4H + 3I + 2J, é dividido por 11.

 Verificamos então o RESTO dessa divisão:

 Se for 0 ou 1, o dígito K é [0] (zero). Se for 2, 3, 4, 5, 6, 7, 8, 9 ou 10, o dígito K é [11 - RESTO]

Fonte: SóMatemática
Thaís Barbosa

É possível dividir um número por zero?

    Se dividirmos um número por zero, a resposta não pode ser zero. Alguns pensam ainda que a divisão por zero é igual ao infinito, pela seguinte razão:
Imagine uma cesta com 8 maçãs. Se cada pessoa pegar quatro maçãs, quantas pessoas tirarão quatro maçãs da cesta? A resposta é DUAS. Mas, e se cada pessoa não tirar nenhuma maçã, quantas poderão pegar as maçãs? Por isso que há a idéia do infinito, visto que infinitas pessoas poderiam "pegar nenhuma" maçã, e essas nunca acabariam. Porém, é um raciocínio incorreto, pois dessa forma infinitas pessoas jamais deixariam a cesta vazia.

Vamos raciocinar da seguinte forma: se 2/0 = x, então 2deveria ser igual a x*0. Mas, qualquer que seja o valor de x, se multiplicarmos por zero jamais iremos obter 2, pois o resultado será sempre zero.
Portanto, não é possível dividir um número por zero. Podemos apenas dividir zero por algum número. Por exemplo:
Quanto vale 0/4?
Nesse caso, 0/4 = x , então 0=4.x , ou seja, x vale zero.
As pessoas não podem tirar maçãs porque a cesta já está vazia.
Outra pergunta interessante seria: Quanto vale 0/0?
0/0=x ou seja, 0=x*0. 
Qualquer valor que colocarmos para x satisfaz a igualdade. Se x pode ser qualquer número, então 0/0 é igual a qualquer coisa. 

Portanto, não é possível dizer quanto vale essa divisão, que é considerada uma indeterminação.

Thaís Barbosa

Por que todo número elevado ao expoente zero é igual a 1?

Para atribuirmos um significado a x⁰, isso dever ser feito de modo a continuar valendo a lei fundamental:
x^{a + b} = x^a x^b Então, fazendo a=0 e tomando qualquer b não nulo, temos:

x^b = x^{0 + b} = x⁰ x^b
mas, considerando x não nulo e b tambem não nulo, temos também que x^b não é nulo e então pode ser simplificado:

x^b = x⁰ x^b

1 = x⁰
Desse modo temos que definir x⁰ = 1 para que continue valendo a lei fundamental.

Ou, seja, podemos dizer que a definição x⁰ = 1 é uma convenção que pode ser justificado pelo cálculo.
Existe também um caso polêmico, quando temos x⁰=1, sendo que x=0. Porém para esse caso não há uma resposta válida universalmente.


Thaís Barbosa

O que significa “ceviana”?

  Ceviana é um segmento de reta que liga um vértice de um triângulo a um ponto qualquer do lado oposto. A altura, a mediana ou a bissetriz do triângulo são cevianas particulares. O nome ceviana é homenagem a Tommaso Ceva, matemático italiano ( 1648-1736 ).

Fonte: Só matemática

Thaís Barbosa

Dicas de cálculo: Como multiplicar um número por 11

Quando o número for de 2 algarismos, basta somar esses 2 algarismos e colocar o resultado no meio deles. Por exemplo, vamos efetuar a seguinte multiplicação: 26 x 11.

Temos o número 26, somando seus 2 algarismos temos 2+6=8. Pronto! Agora é só colocar esse 8 no meio deles:
a resposta é 286. Portanto 26 x 11 = 286.

Outros exemplos:1) 34 x 11
somamos os algarismos do número 34: 3+4=7
colocamos o resultado no meio deles: 374. Portanto 34x11 = 374.

2) 81 x 11
somamos os algarismos do número 81: 8+1=9
colocamos o resultado no meio deles: 891. Portanto 81x11 = 891.

3) 37 x 11
somamos os algarismos do número 37: 3+7=10

Como deu um nº maior que 9, então não podemos colocar todo o número no meio deles. Colocamos apenas o algarismo das unidades (0) no meio deles, e o algarismo da dezena (1) é somado ao primeiro algarismo do número: 407. Portanto 37x11 = 407.

Quando o número for de 3 algarismos, então esse número multiplicado por 11 resultará em um número de 4 algarismos. Por exemplo, vamos efetuar a seguinte multiplicação: 135 x 11.

Temos o número 135. Somando o 1º com o 2º algarismo desse número temos 1+3=4. Somando o 2º com o 3º algarismo desse número temos 3+5=8. Esses 2 resultados serão colocados no meio do número 135, tirando o seu algarismo do meio:
1485. Portanto 135 x 11 = 1485.

Thaís Barbosa

Situação tensa em sala de aula: PRofessor quebra celular de aluna...

Realmente essa situação e bem estressante , celular tocando duas vezes e ainda por cima essa música ruim....acho que ele nem gosta da música....kkkkkk

Depois de visualizado o vídeo só nos resta a pergunta, Será que o professor agiu de maneira correta ou caberia um processo contra ele?

Weine Doidim ROberth

E aí... Se a sua vida dependesse disso, qual botão você apertaria?

Rafael Andrade

Você conhece Gottfried Wilhelm von Leibniz?

Leibniz nasceu em Leipzig, Alemanha, no dia 1o de julho de 1646. Ingressou na Universidade aos quinze anos de idade e, aos dezessete, já havia adquirido o seu diploma de bacharel. Estudou Teologia, Direito, Filosofia e Matemática na Universidade.

Aos vinte anos de idade, já estava preparado para receber o título de doutor em direito. Este lhe foi recusado por ser ele muito jovem. Deixou então Leipzig e foi receber o seu título de doutor na Universidade de Altdorf, em Nuremberg.

Em 1672 foi para Paris onde conheceu Huygens que lhe sugeriu a leitura dos tratados de 1658 de Blaise Pascal se quisesse tornar-se um matemático. Em 1673, visitou Londres, onde adquiriu uma cópia do Lectiones Geometricae de Isaac Barrow e tornou-se membro da Royal Society. Foi devido a essa visita a Londres que apareceram rumores de que Leibniz talvez tivesse visto o trabalho de Newton, que por sua vez o teria influenciado na descoberta do Cálculo, colocando em dúvida a legitimidade de suas descobertas relacionadas ao assunto.

A partir daí, a Matemática estaria bastante presente nas descobertas de Leibniz. Em outra posterior visita a Londres, ele teria levado uma máquina de calcular, de sua invenção. Uma das inúmeras contribuições de Leibniz à Matemática, foi o estudo da aritmética binária, que segundo ele, havia sido utilizada pelos chineses e estaria presente no livro I Ching.

(calculadora de Leibniz)

Como aconteceu com Newton, o estudo de séries infinitas foi muito importante no início de suas descobertas. Relacionando o triângulo de Pascal e o triângulo harmônico, Leibniz percebeu uma maneira de encontrar o resultado de muitas séries infinitas convergentes. A essa altura, ele voltou-se para o trabalho de Blaise Pascal - Traité des sinus du quart de cercle que lhe teria dado um importante insight: a determinação da tangente a uma curva dependia das diferenças das abscissas e ordenadas na medida em que essas se tornassem infinitamente pequenas e que a quadratura, isto é a área, dependia da soma das ordenadas ou retângulos infinitamente finos.

Esse insight levaria Leibniz em 1676 a chegar às mesmas conclusões a que havia chegado Newton alguns anos antes: ele tinha em mãos um método muito importante devido a sua abrangência. Independente de uma função ser racional ou irracional, algébrica ou transcendente - termo criado por Leibniz - as operações de encontrar "somas" (integrais) ou "diferenças" (diferenciais) poderiam ser sempre aplicadas. O destino havia reservado a Leibniz a tarefa de elaborar uma notação apropriada para estas operações, assim como a nomenclatura - Cálculo Diferencial e Cálculo Integral - ambas utilizadas atualmente.

O primeiro trabalho sobre Cálculo Diferencial foi publicado por Leibniz em 1684, antes mesmo do que Newton, sob o longo título Nova methodus pro maximis et minimis, itemque tangentibus, qua nec irrationales quantitates moratur . Nesse trabalho apareceram as fórmulas:

d(xy) = xdy + ydx (derivada do produto)

d(x/y) = (ydx - xdy)/y² (derivada do quociente)

dxⁿ = nx^n-1

Além do Cálculo, Leibniz contribuiu para outras áreas da Matemática. Foi ele quem generalizou o teorema do binômio em Teorema do Multinômio, para expansões do tipo (x + y + z)ⁿ. A primeira referência do método dos determinantes no mundo ocidental também foi feita por ele. Leibniz reelaborou e desenvolveu o conceito de lógica simbólica. Contribuiu também para a teoria de probabilidades e a análise combinatória.

O peso das descobertas e contribuições de Leibniz para o Cálculo e para a Matemática como um todo é tão grande que outras importantes áreas de atuação freqüentemente são deixadas de lado. Não obstante Leibniz é considerado também um dos sete filósofos modernos mais importantes.

Fonte: http://ecalculo.if.usp.br/historia/leibniz.htm

Thaís Barbosa

Piadas do dia

A origem dos sinais

Todos os dias somamos, subtraimos, dividimos, multiplicamos e estabelecemos relações entre números. Mas, de onde vieram esse sinais que utilizamos para indicar tais operações? Eles são tão antigos quanto os numeros?
É sobre isso que falaremos agora

Adição ( + ) e subtração ( - )

    O emprego regular do sinal + ( mais ) aparece na Aritmética Comercial de João Widman d'Eger publicada em Leipzig em 1489.
Entretanto, representavam não à adição ou à subtração ou aos números positivos ou negativos, mas aos excessos e aos déficit em problemas de negócio. Os símbolos positivos e negativos vieram somente ter uso geral na Inglaterra depois que foram usados por Robert Recorde em 1557.Os símbolos positivos e negativos foram usados antes de aparecerem na escrita. Por exemplo: foram pintados em tambores para indicar se os tambores estavam cheios ou não.

    Os antigos matemáticos gregos, como se observa na obra de Diofanto, limitavam-se a indicar a adição juntapondo as parcelas - sistema que ainda hoje adotamos quando queremos indicar a soma de um número inteiro com uma fração. Como sinal de operação mais usavam os algebristas italianos a letra P, inicial da palavra latina plus.

Multiplicação ( . ) e divisão ( : )

    O sinal de X, como que indicamos a multiplicação, é relativamente moderno. O matemático inglês Guilherme Oughtred empregou-o pela primeira vez, no livro Clavis Matematicae publicado em 1631. Ainda nesse mesmo ano, Harriot, para indicar também o produto a efetuar, colocava um ponto entre os fatores. Em 1637, Descartes já se limitava a escrever os fatores justapostos, indicando, desse modo abreviado, um produto qualquer. Na obra de Leibniz escontra-se o sinal 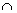 para indicar multiplicação: esse mesmo símbolo colocado de modo inverso indicava a divisão.

    O ponto foi introduzido como um símbolo para a multiplicação por G. W. Leibniz. Julho em 29, 1698, escreveu em uma carta a John Bernoulli: "eu não gosto de X como um símbolo para a multiplicação, porque é confundida facilmente com x; freqüentemente eu relaciono o produto entre duas quantidades por um ponto . Daí, ao designar a relação uso não um ponto mas dois pontos, que eu uso também para a divisão."
As formas a/b e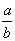 , indicando a divisão de a por b, são atribuídas aos árabes: Oughtred, e, 1631, colocava um ponto entre o dividendo o divisor. A razão entre duas quantidades é indicada pelo sinal :, que apareceu em 1657 numa obra de Oughtred. O sinal ÷, segundo Rouse Ball, resultou de uma combinação de dois sinais existentes - e :

Sinais de relação ( =, < e > )

    Robert Recorde, matemático inglês, terá sempre o seu nome apontado na história da Matemática por ter sido o primeiro a empregar o sinal = ( igual ) para indicar igualdade. No seu primeiro livro, publicado em 1540, Record colocava o símbolo 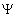entre duas expressões iguais; o sinal = ; constituído por dois pequenos traços paralelos, só apareceu em 1557. Comentam alguns autores que nos manuscritos da Idade Média o sinal = aparece como uma abreviatura da palavra est.

    Guilherme Xulander, matemático alemão, indicava a igualdade , em fins do século XVI, por dois pequenos traços paralelos verticais; até então a palavra aequalis aparecia, por extenso, ligando os dois membros da igualdade.

    Os sinais > ( maior que ) e < ( menor que ) são devidos a Thomaz Harriot, que muito contribuiu com seus trabalhos para o desenvolvimento da análise algébrica.

Thaís Barbosa